datastruct-tut

Python

Binary Trees

Introduction to Binary Search Tree’s

An issue with every data structure so far is the time it takes to find any given item. With stacks and queues whether we implement them with arrays or linked lists it takes O(n) time to find any given node in the data structure.

Luckily there is a data structure that it is great at sorting and finding data. It’s a Binary Search Tree or BST for short. BST’s are extremely efficient at searching for nodes.

Recursion

But before we talk in depth about BST’s we must discussion recursion. Recursive algorithm’s are often used with BST’s. Recall back in the very first Introduction module when talking about Big O notation a recursive function that calculated the fibonacci sequence was introduced. Here is that function again:

 def fib(n):
   # base case
   if n <= 1 : return n
   # recurse to solve the rest
   return fib(n - 2) + fib(n - 1)

This function has two lines, the base case, and the recursive algorithm.

When creating a recursive algorithm you want to consider when is your problem solved, with a fibonacci sequence it is solved when we’ve counted down all the way to 1.

You also want to think about how you can solve one simple piece of the problem, and hand off the rest of the problem to a function, knowing and trusting that the function can solve the rest.

In this case we call fib again with n - 2 as a parameter, and add it’s result to a second call to fib with n - 1 as a parameter.

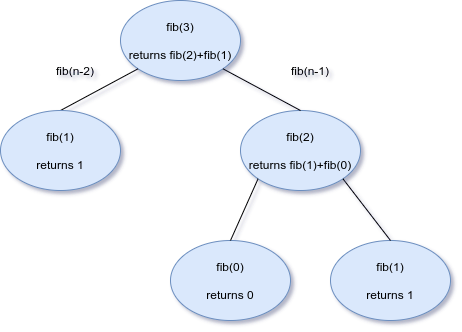
Think on what happens if you called fib(3)

fib(3) would check if n <= 1, it’s not so it proceeds to the next line.
fib(3) would then call fib(1) and fib(2) and add their results together.
fib(1) would check if n <= 1, it is so it returns n, which is 1.
fib(2) would check if n <= 1, it’s not so it proceeds to the next line.
fib(2) would call fib(0) and fib(1) and add their results.
fib(0) would check if n <= 1, it is so it would return 0.
fib(1) would check if n <= 1, it is so it would return 1.
fib(2) now has the results of fib(0) and fib(1), 0 and 1 respectively. It will add those and return the result which is 1.
fib(3) now has the results of fib(1) and fib(2), which is 1, and 1 respectively. It will add them together and return the result which is two.
The solution to fib(3) is two.

Here is a simple tree which depicts this sequence of events.

Thinking recursively isn’t easy, but you need it for some algorithms. BST’s are one of those cases.

BST - basics

A BST is somewhat similar to a linked list in that you have discreet nodes which point to other nodes. Like a singly linked list node links only go one way, not both ways like in a doubly linked list.

At the top of your tree you have the root node. It will have links to two nodes, a left node and a right node. Each node below the root is the same. Nodes that have no child links are called leaves. This is perhaps best shown with a picture.

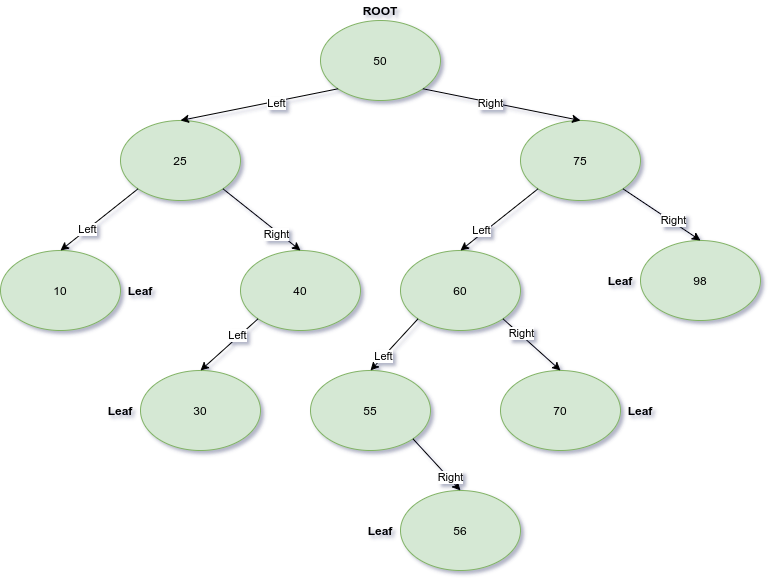
The pictured BST has the node with a value of 50 set as the root of the tree. To the left of the root node are all values smaller than itself, to the right are all values larger. No duplicates are allowed.

Each node of this BST can be viewed as a subtree with itself as the root. For example if we got to the left of the root node, and view the node with a value of 25 as the root or our subtree you can see it has all of the same properties discussed for the original root.

This property is how we deal with a bst using recursion, each pass we view the next node as it’s own subtree.

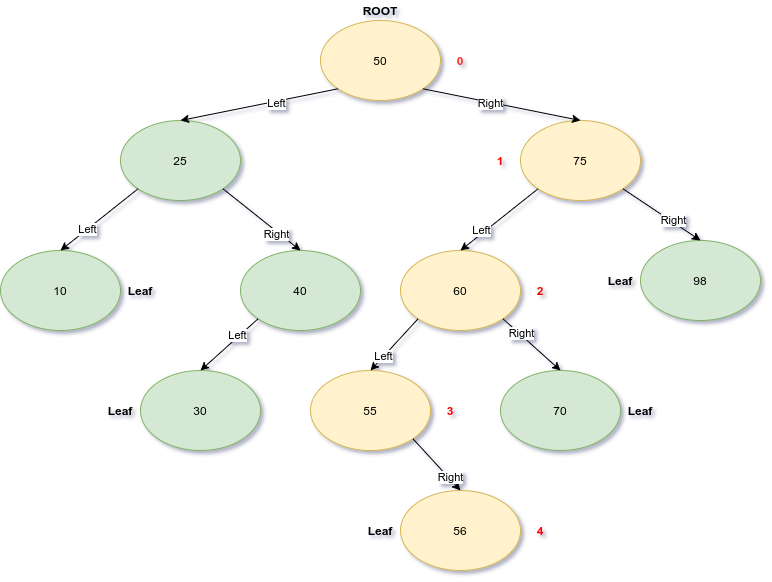
A given BST’s height is found by counting the number of hops it takes to get from the root to the furthest leave. We start at zero so a tree with a root and no child links as a height of 0. The height of the example tree above is depicted below showing it has a height of 4.

For BST’s to be efficient when searching we need to keep them balanced. To determine if a tree is balanced we check the height of both sides and ensure that neither side has a height difference more than 1. This must also hold true for each subtree. So is our example BST balanced? Let’s take a look visually. To do this we will find the height of the left and right subtrees, and check that they aren’t more than 1 different.

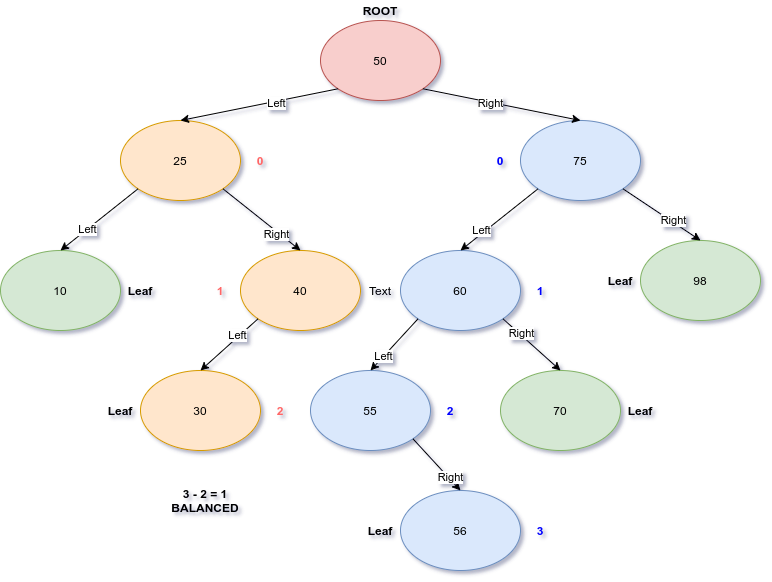
As depicted these two subtrees are balanced but we have to keep checking to see if the rest are balanced as well. We will descend down the right side and check the left and right subtrees under node 75.

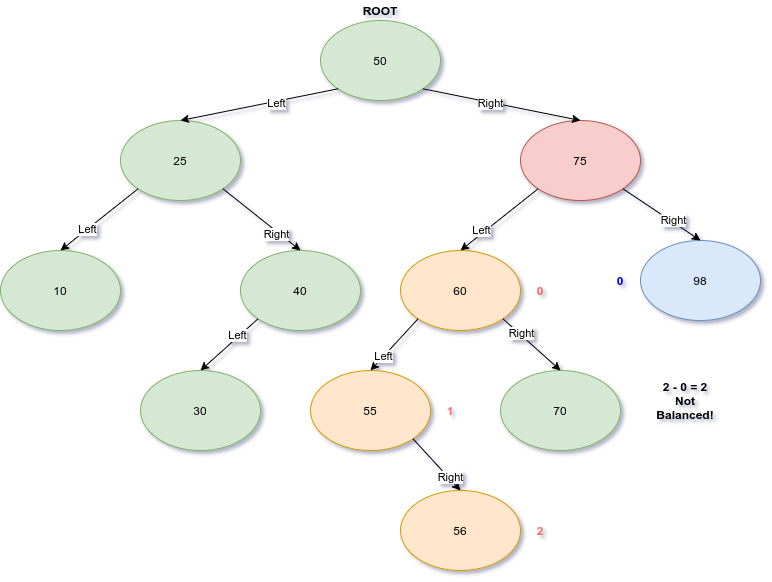
Oops! This subtree is not balanced on the left and right sides. This will hurt the efficiency of searching this BST. This means the overall tree is not balanced. There are efficient ways to balance tree’s, which involves rotating nodes to shift the roots of subtrees but we won’t discuss this in depth here. For fun though here is a gif that shows what balancing a tree looks like.

Coding Challenge

For this modules challenge, like with the linked lists. We will build up a BST class with each individual module and then apply it to a problem.

You will be given a sorted list of States that have been decimated by a zombie apocalypse. Your task will be to build a balanced tree from this list so that users can query which states they should not be visiting.

BST Skeleton

We’ll start off with a skeleton of a BST class.

class BST:
  '''A Binary Search Tree.'''

  class Node:
    '''An individual node within a BST.'''

    def __init__(self, data):
      '''Initialize a node with no known links.'''

      self.data = data
      self.left = None
      self.right = None

  def __init__(self):
    '''Initialize an empty BST.'''

    self.root = None

Helper functions

We could really use some functions that help us debug and round out the features of our BST more. We are going to create two dunder functions to teach python how to iterate over this data structure forwards and backwards. We are also going to create a function that reports on the height of the BST. These will give you an idea of how we will use recursion to work with BSTs and the general pattern for how we’ll be writing functions.

Iteration

When we do an in order traversal of a BST we want to print all nodes in order of least to greatest. Considering that lesser nodes are on the left, and greater nodes are on the right the way we might traverse a BST is:

Descend down the left side.
When we hit a leaf yield the data.
Descend down the right side.
When we hit a leaf yield the data.

We are going to use the __iter__ dunder function to call a recursive _traverse_forward.

__iter__ will just call the recursive algorithm like this:

def __iter__(self):
  '''Teach python how to iterate over our data structure'''

  yield from self._traverse_forward(self.root) # start at the root

The actual _traverse_forward will follow the pattern outlined above:

def _traverse_forward(self, node):
  '''
  If a node is none do nothing, otherwise travel down
  the left side then the right side
  '''

  if node is not None:
    # travel down the left, this will stop when it heads a node
    # with no left node
    yield from self._traverse_forward(node.left)
    yield node.data
    # Do the same on the right
    yield from self._traverse_forward(node.right)

What this does is call itself going down the left side until it lands on a node that is None, once it hits none it pops up one node and returns that nodes data (this would be the left most leaf). Then it attempts to do the same down the right side.

To iterate backwards we need to write a __reversed__ function. It is exactly the same only we traverse down the right side, then the left. I’ll let you write __reversed__ yourself.

Getting a tree’s height.

The next function we’ll need is one that reports the BST’s height. Again we’ll use a function to call anther recursive function (that’s a pattern that will hold).

What we’ll do is add up the height of all subtrees recursively and return the height of the tallest one.

def get_height(self):
  '''Determine the height of a BST.'''

  # If it's an empty tree our height is zero
  if self.root is None:
    return 0
  else:
    return self._get_height(self.root)

This is the recursive part.

def _get_height(self, node):
  '''
  The height of any subtree is 1 plus the height of either the left
  or right subtree, whichever is greater.
  '''

  # This is the base case, we are at a Node that is None
  if node is None:
    return 0
  else:
    # A lot like __iter__, we just go down one side at a time.
    # Adding up their heights
    sum_right = 1 + self._get_height(node.right)
    sum_left = 1 + self._get_height(node.left)
    # We return whichever sum is greatest.
    return sum_right if sum_right > sum_left else sum_left

Inserting into a BST

With those helper functions in hand to help us debug the next thing we need to be able to do is insert values into a BST. By the way, if our tree is balanced, the worst case performance is O(log₂n).

The steps.

Create a node
Check for an empty tree
If it’s empty, just make the node the root.
If it’s not, call a recursive insert function.

The recursive insert

Check that the node isn’t equal to the value we are inserting
If they are equal abort, we can’t have duplicates
If it’s value is less than this node, it goes on the left. Check if we have a child node to the left. If not insert it, otherwise call insert again on the left node.
If it’s value is greater than this node, it goes on the right. Check if we have a child node to the right. If not insert it, otherwise call insert again on the right node.

Write an insert function that does the first group of steps.

Write a recursive _insert function that does the last group of steps.

Check your solution against bst-insert.py

Searching a BST

The next step needed for this coding challenge is the ability to search for values. Like inserting, searching a balanced BST has a performance of O(log₂n). To search our BST we will write a dunder method __in__. This let’s use use the python keyword in to check if a value is in the BST.

The actual code in the __in__ function will just call a recursive function called _contains and return it’s result.

_contains will take the data it’s looking for and the node it’s to operate on.

The steps _contains should be taking.

Check for an empty node. If it is empty return False.
Check if the node has our data. If it does return True.
Check if data is less than or greater than our current node.
Recurse down the left or right side respectively based on the check above.

Write the __in__ function.

Write the _contains function.

Check your solution against bst_search.py

Combine it all

With these in hand we have a basic BST that will solve the problem efficiently. Because the data you are being given is a sorted array, you’ll want the root of your BST to be the middle value of the array.

You will write a recursive function that inserts data from the middle of the array. Remember each subtree needs to also have it’s root as the middle of a sub-array. This function will be called from a create_bst() function.

Here is some starter code, it has an interactive portion commented out. Once you’ve done enough debugging that you feel like it’s solved. You can uncomment the interactive portion and test it out.

bst-start-code.py

Check your solution against bst-completed.py

Previous Module